Contoh Soal Kesebangunan Dan Kekongruenan Berdiri Datar Dan Penyelesaiannya
Rumus Matematika Dasar sudah pernah menawarkan ulasan bahan mengenai Kesebangunan dan Kekongruenan Bangun Datar Matematika. Nah, untuk memperdalam pemahaman kalian mengenai bahan tersebut, di sini kami akan menawarkan beberapa rujukan soal yang bias kalian gunakan untuk berlatih di rumah. Pada masing-masing soal akan diberikan klarifikasi mengenai bagaimana cara menyelesaikannya. Namun untuk beberapa soal-soal yang lain kalian harus mengerjakannya sendiri atau bisa juga sambil didampingi oleh orangtua atau abang kalian semoga bisa bertanya apabila menjumpai kesulitan dalam memahami cara penyelelesaian soal yang diberikan. Yuk, mari eksklusif saja kita simak rujukan duduk perkara yang pertama:
Contoh Soal Kesebangunan dan Kekongruenan Bangun Datar
Contoh Soal 1:
Perhatikan gambar dua buah belah ketupat di bawah ini, apakah kedua berdiri tersebut sanggup dinyatakan kongruen?
Penyelesaian:
Untuk menjawab soal tersebut, kalian harus mengingat kembali akan sifat-sifat berdiri datar yang dimiliki oleh belah ketupat, yaitu:
a. Semua sisi sama panjang dan sepasang-sepasang sejajar.
b. sudut-sudut yang berhadapan sama besar dan terbagi dua sama besar.
Pada belah ketupat ABCD diatas, diketahui bahwa AB = BC = CD = AD = 6 cm,
Sudut A = sudut C = 400, dan sudut B = sudut D = 1400 (sudut-sudut yang berhadapan)
Pada belah ketupat EFGH diatas, diketahui bahwa EF = FG = GH = EH = 6 cm,
Sudut E = sudut G = 400, dan sudut F = sudut H = 1400
Dari uraian tersebut sanggup diperoleh:
AB/EF = BC/FG = CD/GF = AD=EH = 1
sudut A = sudut C = Sudut E = sudut G = 400
sudut B = sudut D = sudut F = sudut H = 1400
Karena sisi-sisinya yang bersesuaian mempunyai ukuran sama panjang serta sudut-sudut yang bersesuaian sama besarnya, maka berdiri ABCD dan EFGH bisa dikatakan kongruen.
Contoh Soal 2:
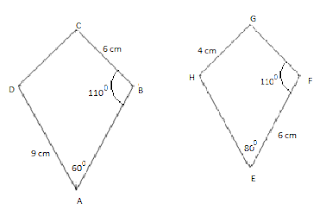
Perhatikan gambar layang-layang di bawah ini:
Apakah layang-layang ABCD dan EFGH sebangun?
Penyelesaian:
Layang-layang mempunyai sepasang sudut berhadapan yang sama besar. Sifat tersebut sanggup kita gunakan untuk mencari sudut-sudut yang belum diketahui besarnya pada sebuah laying-layang.
Untuk layang-layang ABCD:
Sudut D = Sudut B = 1100 dan sudut A = 600
maka sudut C = 3600 – (110 + 110 + 80) 0 = 800
Untuk layang-layang EFGH:
Sudut H = Sudut F = 1100 dan sudut G = 800
maka sudut E = 3600 – (110 + 110 + 80) 0 = 600
Dengan demikian kita bisa menyimpulkan bahwa:
Sudut A = sudut E, sudut B = sudut F, sudut C = sudut G, dan sudut D = sudut H. dan ternyata sudut-sudut yang bersesuaian pada kedua laying-layang tersebut sama besar.
Untuk layang-layang ABCD, diketahui bahwa CD = BC = 6 cm dan AB = AD = 9 cm
Untuk layang-layang EFGH, diketahui bahwa GH = FG = 4 cm dan EH = EF = 6 cm
Sehingga sanggup diperoleh:
BC/FG = DC/GH = 6/4 = 3/2
AD/EH = AB/EF = 9/6 = 3/2
Karena sudut-sudutnya sama besar dan perbandingan sisi-sisinya bersesuaian maka sanggup kita simpulkan bahwa laying-layang ABCD bersifat sebangun dengan EFGH.
Jika kalian sudah paham dengan klarifikasi soal di atas, kini saatnya kalian berlatih untuk mengerjakan soal-soal di bawah ini:
Soal Latihan 1:
Perhatikan gambar berikut:
Apakah trapesium ABCD dan trapesium EFGH sebangun? Jelaskan jawabanmu!
Soal Latihan 2:
a. Apakah persegi panjang KLMN sebangun dengan persegi panjang PQRS?
b. Apakah persegi panjang KLMN kongruen dengan persegi panjang PQRS?
Soal Latihan 3:
Diantara bangun-bangun berikut, manakah yang sudah niscaya sebangun?
a. dua persegi
b. dua segitiga samakaki
c. dua segitiga sama sisi
d. dua segitiga siku-siku
e. dua belah ketupat
f. dua segienam beraturan
g. dua lingkaran
h. dua layang-layang
Nah, itulah beberapa Contoh Soal Kesebangunan dan Kekongruenan Bangun Datar yang bisa kalian coba kerjakan untuk menguji kemampuan kalian mengenai bahan tersebut. Teruslah berlatih dan tetap semangat mencar ilmu semoga kalian bisa mengerjakan soal-soal mengenai kesebangunan dan kekongruenan berdiri datar dengan bentuk-bentuk yang lain. Terimakasih telah menyimak bahan ini hingga akhir, hingga jumpa lagi.